决策树
决策树(Decision Tree)是一种简单但是广泛使用的分类器。通过训练数据构建决策树,可以高效的对未知的数据进行分类。决策数有两大优点:1)决策树模型可以读性好,具有描述性,有助于人工分析;2)效率高,决策树只需要一次构建,反复使用,每一次预测的最大计算次数不超过决策树的深度。
如何预测
先看看下面的数据表格: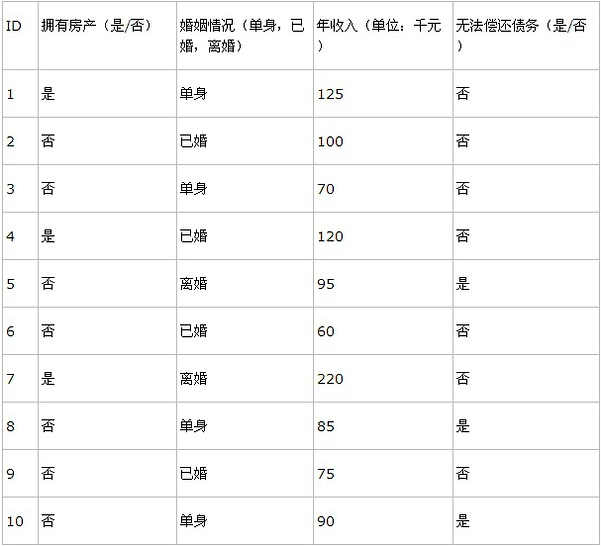
上表根据历史数据,记录已有的用户是否可以偿还债务,以及相关的信息。通过该数据,构建的决策树如下: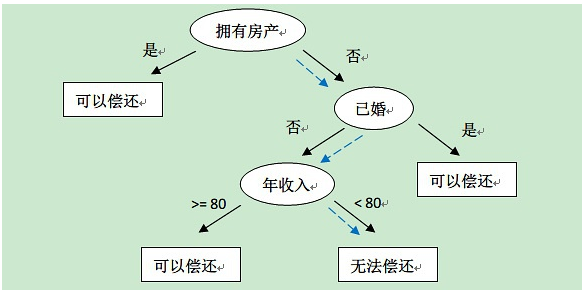
比如新来一个用户:无房产,单身,年收入55K,那么根据上面的决策树,可以预测他无法偿还债务(蓝色虚线路径)。从上面的决策树,还可以知道是否拥有房产可以很大的决定用户是否可以偿还债务,对借贷业务具有指导意义。
基本步骤
决策树构建的基本步骤如下:
1.开始,所有记录看作一个节点
2.遍历每个变量的每一种分割方式,找到最好的分割点
3.分割成两个节点N1和N2
4.对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止
决策树的变量可以有两种:
1) 数字型(Numeric):变量类型是整数或浮点数,如前面例子中的“年收入”。用“>=”,“>”,“<”或“<=”作为分割条件(排序后,利用已有的分割情况,可以优化分割算法的时间复杂度)。
2) 名称型(Nominal):类似编程语言中的枚举类型,变量只能重有限的选项中选取,比如前面例子中的“婚姻情况”,只能是“单身”,“已婚”或“离婚”。使用“=”来分割。
如何评估分割点的好坏?如果一个分割点可以将当前的所有节点分为两类,使得每一类都很“纯”,也就是同一类的记录较多,那么就是一个好分割点。比如上面的例子,“拥有房产”,可以将记录分成了两类,“是”的节点全部都可以偿还债务,非常“纯”;“否”的节点,可以偿还贷款和无法偿还贷款的人都有,不是很“纯”,但是两个节点加起来的纯度之和与原始节点的纯度之差最大,所以按照这种方法分割。构建决策树采用贪心算法,只考虑当前纯度差最大的情况作为分割点。
量化纯度
前面讲到,决策树是根据“纯度”来构建的,如何量化纯度呢?这里介绍三种纯度计算方法。如果记录被分为n类,每一类的比例P(i)=第i类的数目/总数目。还是拿上面的例子,10个数据中可以偿还债务的记录比例为P(1) = 7/10 = 0.7,无法偿还的为P(2) = 3/10 = 0.3,N = 2。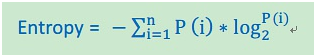
纯度差,也称为信息增益(Information Gain),公式如下: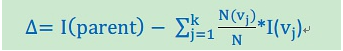
其中,I代表不纯度(也就是上面三个公式的任意一种),K代表分割的节点数,一般K = 2。vj表示子节点中的记录数目。上面公式实际上就是当前节点的不纯度减去子节点不纯度的加权平均数,权重由子节点记录数与当前节点记录数的比例决定。
停止条件
决策树的构建过程是一个递归的过程,所以需要确定停止条件,否则过程将不会结束。一种最直观的方式是当每个子节点只有一种类型的记录时停止,但是这样往往会使得树的节点过多,导致过拟合问题(Overfitting)。另一种可行的方法是当前节点中的记录数低于一个最小的阀值,那么就停止分割,将max(P(i))对应的分类作为当前叶节点的分类。
过渡拟合
采用上面算法生成的决策树在事件中往往会导致过滤拟合。也就是该决策树对训练数据可以得到很低的错误率,但是运用到测试数据上却得到非常高的错误率。过渡拟合的原因有以下几点:
噪音数据:训练数据中存在噪音数据,决策树的某些节点有噪音数据作为分割标准,导致决策树无法代表真实数据。
缺少代表性数据:训练数据没有包含所有具有代表性的数据,导致某一类数据无法很好的匹配,这一点可以通过观察混淆矩阵(Confusion Matrix)分析得出。
多重比较(Mulitple Comparition):举个列子,股票分析师预测股票涨或跌。假设分析师都是靠随机猜测,也就是他们正确的概率是0.5。每一个人预测10次,那么预测正确的次数在8次或8次以上的概率为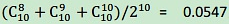
,只有5%左右,比较低。但是如果50个分析师,每个人预测10次,选择至少一个人得到8次或以上的人作为代表,那么概率为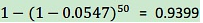
,概率十分大,随着分析师人数的增加,概率无限接近1。但是,选出来的分析师其实是打酱油的,他对未来的预测不能做任何保证。上面这个例子就是多重比较。这一情况和决策树选取分割点类似,需要在每个变量的每一个值中选取一个作为分割的代表,所以选出一个噪音分割标准的概率是很大的。
优化方案1:修剪枝叶
决策树过渡拟合往往是因为太过“茂盛”,也就是节点过多,所以需要裁剪(Prune Tree)枝叶。裁剪枝叶的策略对决策树正确率的影响很大。主要有两种裁剪策略。
前置裁剪 在构建决策树的过程时,提前停止。那么,会将切分节点的条件设置的很苛刻,导致决策树很短小。结果就是决策树无法达到最优。实践证明这中策略无法得到较好的结果。
后置裁剪 决策树构建好后,然后才开始裁剪。采用两种方法:1)用单一叶节点代替整个子树,叶节点的分类采用子树中最主要的分类;2)将一个字数完全替代另外一颗子树。后置裁剪有个问题就是计算效率,有些节点计算后就被裁剪了,导致有点浪费。
优化方案2:K-Fold Cross Validation
首先计算出整体的决策树T,叶节点个数记作N,设i属于[1,N]。对每个i,使用K-Fold Validataion方法计算决策树,并裁剪到i个节点,计算错误率,最后求出平均错误率。这样可以用具有最小错误率对应的i作为最终决策树的大小,对原始决策树进行裁剪,得到最优决策树。
优化方案3:Random Forest
Random Forest是用训练数据随机的计算出许多决策树,形成了一个森林。然后用这个森林对未知数据进行预测,选取投票最多的分类。实践证明,此算法的错误率得到了经一步的降低。这种方法背后的原理可以用“三个臭皮匠定一个诸葛亮”这句谚语来概括。一颗树预测正确的概率可能不高,但是集体预测正确的概率却很高。
准确率估计
决策树T构建好后,需要估计预测准确率。直观说明,比如N条测试数据,X预测正确的记录数,那么可以估计acc = X/N为T的准确率。但是,这样不是很科学。因为我们是通过样本估计的准确率,很有可能存在偏差。所以,比较科学的方法是估计一个准确率的区间,这里就要用到统计学中的置信区间(Confidence Interval)。
设T的准确率p是一个客观存在的值,X的概率分布为X ~ B(N,p),即X遵循概率为p,次数为N的二项分布(Binomial Distribution),期望E(X) = Np,方差Var(X) = Np(1-p)。由于当N很大时,二项分布可以近似有正太分布(Normal Distribution)计算,一般N会很大,所以X ~ N(np,np(1-p))。可以算出,acc = X/N的期望E(acc) = E(X/N) = E(X)/N = p,方差Var(acc) = Var(X/N) = Var(X) / N2 = p(1-p) / N,所以acc ~ N(p,p*(1-p)/N)。这样,就可以通过正太分布的置信区间的计算方式计算执行区间了。
正太分布的置信区间求解如下:
1) 将acc标准化,即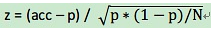
2) 选择置信水平α= 95%,或其他值,这取决于你需要对这个区间有多自信。一般来说,α越大,区间越大。
3) 求出 α/2和1-α/2对应的标准正太分布的统计量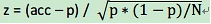

(均为常量)。然后解下面关于p的不等式。acc可以有样本估计得出。即可以得到关于p的执行区间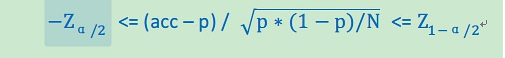
another example:
有一天,小明无聊,对宿舍玩CS的舍友进行统计,结果刚记下四行,被舍友认为影响发挥,给踢到床下去了,让我们看看可怜的小明的记录:
为了对得起小明记录的这四条记录,我们对其进行决策树分析,从数据中看:
- 如果一个玩家子弹很多,那么即使血少他也会战斗,如果子弹少的话,即使血多,他也会逃跑隐蔽起来;
- 那我们再看子弹少的情况下,武器靠刀子,当血多时候,他还是会打一打得,但是血少,就立即逃跑隐蔽了。
这是我们大脑直觉上去分析,既然本文我是想聊一聊决策树,那么我们就用决策树来对小明的这些数据小试牛刀一下,顺便来慰藉一下小明(从小到大我们已经看过无数的小明了,这里再借用一下大度的小明)。
我们现在将数据分为两块:
X = {武器类型,子弹数量,血}
Y = {行为}
我们建立这颗决策树的目的就是,让计算机自动去寻找最合适的映射关系,即:Y = f(X),所谓听上去大雅的“数据挖掘”学科,干得也差不多就是这回事,X我们称之为样本,Y我们称之为结果(行为/类)。
样本是多维的,X = {x1,x2,…xn},如本例:X = {x1=武器类型,x2=子弹数量,x3=血},我们就是要通过这些不同维度的观测记录数据,和应对的不同结果,找到规律(映射关系),举个例子:
X = {天气,温度,湿度,女友约会} -> Y = {是否答应兄弟下午去打篮球}
X = {老妈说你是胖子,老婆说你是胖子,自己上秤评估自己体重} -> Y = {去办健身卡减肥}
这样来说,X的多维不同的数据,大个比方,更像是很多大臣,那么我们就是要根据这些大臣的意见,来决策,如本例:
左大臣:武器类型
中大臣:子弹数量
右大臣:血
这些大臣每个人都有想法,左右着皇帝继续战斗还是撤退,但是三个也不能全信,那么我们就要根据他们的陈年老帐(训练样本)来评判他们的话语的重要性,当然,优先级高的肯定话语是有重量的,我们先提前来预览一下这个例子训练出来的决策树的样子: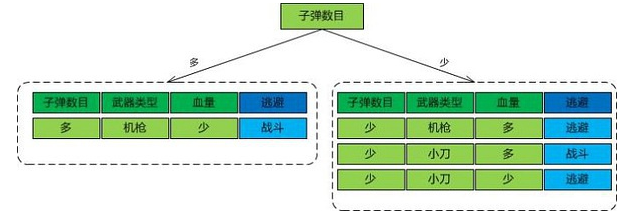
这个根据小明的数据训练出来的决策树是不是和我们刚才拍脑门分析出来的结果差不多呢?看,子弹多就开打,子弹少,在看看用什么武器,如果又没子弹又用机枪,那铁定跑,如果用小刀,在掂量一下自己血厚不厚,厚则打,不厚则逃,看来决策树分析的结果还是可以的啊,接下来,我们来研究研究,计算机(这个只会重复人们给它设定的代码的家伙)是如何实现这样的分析的。
既然是三个大臣提意见{左大臣:武器类型,中大臣:子弹数量,右大臣:血},那么我们要分析一下历史数据(训练数据)他们哪个话更靠谱:
我们先单纯的看看左大臣的历史战绩(统计训练样本):
机枪 -> 战斗
机枪 -> 逃跑
小刀 -> 战斗
小刀 -> 逃跑
用机枪,你战斗逃跑的概率都是50%,用刀子,你亦似打似逃!看来这个大臣立场不坚定啊!
再看看中大臣的:
子弹多 -> 战斗
子弹少 -> 逃跑
子弹少 -> 战斗
子弹少 -> 逃跑
用机枪,你战斗概率是100%,用刀子,你33.3%打,你66.6%撤!这位大臣似乎坚定了一些。
再看看右大臣的:
血少 -> 战斗
血多 -> 逃跑
血多 -> 战斗
血少 -> 逃跑
和左大臣一样,立场不坚定,50:50啊!
这样,中大臣的话的重量就提升了,因此决策书的第一层就重用中大臣吧(中大臣变成一品大员)
计算机是怎么来做到这一步的呢?且让我一步一步讲:
决策树训练中,有一个很重要的尺子,来衡量大臣的可信度,这个尺子,就是信息论的熵(Entropy),这个熵是何许人也,竟然朝廷大臣的可信度竟然用次来衡量,让我们对他做个自我介绍吧:
熵,洋名为(Entropy),乃测量信息的混乱程度为职,纵横科学界各门学术之中,为人低调,俭朴,就一个很短的公式:E = sum(-p(I)*log(p(I))),I=1:N(N类结果,如本例两种,战斗或逃跑),当信息一致,所有样本都属于一个类别I,那么熵为0,如果样本完全随机,那么熵为1,表明这个臣子对这种状态的预测就是胡言乱语。
OK,熵,告诉我你对这个数据的看法:
E(机枪) = -(1/2)Log2(1/2) - (1/2)Log(1/2) = 0.5 + 0.5 = 1
E(小刀) = -(1/2)Log2(1/2) - (1/2)Log(1/2) = 0.5 + 0.5 = 1
E(子弹多) = -(1/1)Log2(1/1) - (0/1)Log(0/1) = 0 + 0 = 0
E(子弹少) = -(1/3)Log2(1/3) - (2/3)Log(2/3) = 0.5283 + 0.39 = 0.9183
E(血多) = -(1/2)Log2(1/2) - (1/2)Log(1/2) = 0.5 + 0.5 = 1
E(血少) = -(1/2)Log2(1/2) - (1/2)Log(1/2) = 0.5 + 0.5 = 1
那么我们怎么用这个熵来衡量大臣(每维数据)的可信度呢,这里还要再引出一位仁兄,其是熵的上级,他熟知熵的能力,很会用熵,他就是信息增益(Information Gain),我们来看看这位上级是如何用熵来衡量的:
Gain(Sample,Action) = E(sample) - sum(|Sample(v)|/Sample * E(Sample(v)))
OK,Information Gain,说说你是怎么评估这个例子的三位大臣的!
Gain(武器类型) = E(S) - (2/4)E(机枪) - (2/4)E(小刀) = 1 - (2/4)1 - (2/4)1 = 0
Gain(子弹数量) = E(S) - (1/4)E(子弹多) - (3/4)E(子弹少) = 1 - (1/4)0 - (3/4)0.9183 = 0.3113
Gain(血量) = E(S) - (2/4)E(血多) - (2/4)E(血少) = 1 - (2/4)1 - (2/4)1 = 0
接着,计算机通过信息增益结果,选择最大的,作为一品大员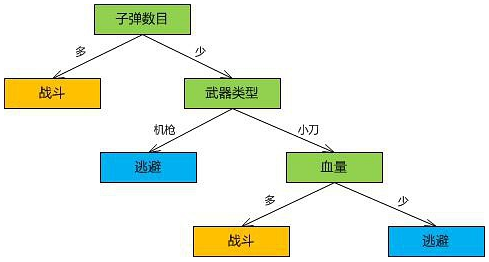
且看一品大员对子弹多的情况下料事如神(暂且不说本例样本少),但是其在子弹少的情况下,决策还是不行的,那么,再用同样的方法,再去选择二品,三品,这就是决策树的训练。